Coursera - Computer Science: Programming With A Purpose

Write a program Divisors.java to compute the greatest common divisor and related functions on integers:

• The greatest common divisor (gcd) of two integers a and b is the largest positive integer that is a divisor of both a and b. For example, gcd(1440, 408) = 24 because 24 is a divisor of both 1440 and 408 (1440 = 24 * 60, 408 = 24 * 17) but no larger integer is a divisor of both. By convention, gcd(0,0) = 0.
• The least common multiple (lcm) of two integers a and b is the smallest positive integer that is a multiple of both a and b. For example, lcm(56, 96) = 672 because 672 is a multiple of both 56 and 96 (672 = 56 * 7 = 96 * 12) but no smaller positive number is a multiple of both. By convention, if either a or b is 0, then lcm(a, b) = 0.
• Two integers are relatively prime if they share no positive common divisors (other than 1). For example, 221 and 384 are not relatively prime because 17 is a common divisor.
• Euler’s totient function ϕ(n) is the number of integers between 1 and n that are relatively prime with n. For example, ϕ(9) = 6 because the six numbers 1, 2, 4, 5, 7, and 8 are relatively prime with 9. Note that if n ≤ 0, then ϕ(n) = 0.

To do so, organize your program according to the following public API:

public class Divisors {

    // Returns the greatest common divisor of a and b.
    public static int gcd(int a, int b)

    // Returns the least common multiple of a and b.
    public static int lcm(int a, int b)

    // Returns true if a and b are relatively prime; false otherwise.
    public static boolean areRelativelyPrime(int a, int b)

    // Returns the number of integers between 1 and n that are
    // relatively prime with n.
    public static int totient(int n)

    // Takes two integer command-line arguments a and b and prints
    // each function, evaluated in the format (and order) given below.
    public static void main(String[] args)
}

Here are some sample executions:

~/Desktop/functions> java Divisors 1440 408
gcd(1440, 408) = 24
lcm(1440, 408) = 24480
areRelativelyPrime(1440, 408) = false
totient(1440) = 384
totient(408) = 128

~/Desktop/functions> java Divisors 987 610
gcd(987, 610) = 1
lcm(987, 610) = 602070
areRelativelyPrime(987, 610) = true
totient(987) = 552
totient(610) = 240

Use the following algorithms to implement the corresponding functions.

• Greatest common divisor. Implement an iterative version of Euclid’s algorithm. To compute the greatest common divisor of a and b:
  • Replace (a, b) with (abs(a), abs(b)).
  • Repeatedly replace (a, b) with (b, a % b) until the second integer in the pair is zero.
  • Return the first integer in the pair as the gcd.

  

• Least common multiple. Use the following formula, which relates the gcd and lcm functions: lcm(a, b) = (abs(a) * abs(b)) / gcd(a, b) To avoid preventable arithmetic overflow, perform the division before the multiplication. Recall that lcm(0, 0) = 0.

  

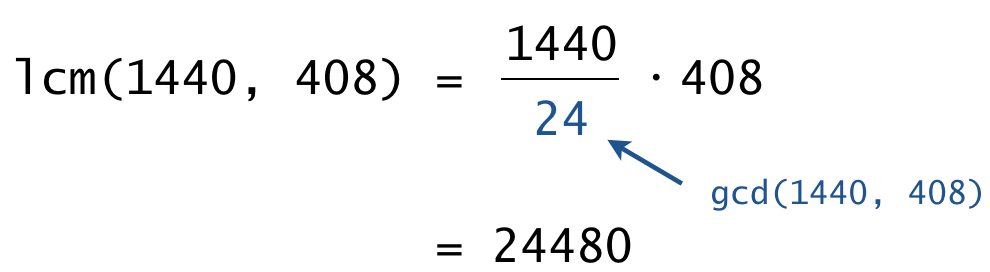
• Relatively prime. Two integers a and b are relatively prime if and only if gcd(a, b) = 1.
• Euler’s totient function. Use the definition and call areRelativelyPrime() for each positive integer between 1 and n.

The greatest common divisor and least common multiple functions arise in a variety of applications, including reducing fractions, modular arithmetic, and cryptography. Euler’s totient function plays an important role in number theory, including Euler’s theorem and cyclotomic polynomials.

Note: the above description is copied from Coursera and converted to markdown for convenience

Solution:

public class Divisors {

    // Returns the greatest common divisor of a and b.
    public static int gcd(int a, int b) {
        a = Math.abs(a);
        b = Math.abs(b);
        while (b != 0) {
            int mod = a % b;
            a = b;
            b = mod;
        }
        return a;
    }

    // Returns the least common multiple of a and b.
    public static int lcm(int a, int b) {
        if ((a == 0) && (b == 0)) {
            return 0;
        }
        return Math.abs(a) * (Math.abs(b) / gcd(a, b));
    }

    // Returns true if a and b are relatively prime; false otherwise.
    public static boolean areRelativelyPrime(int a, int b) {
        return gcd(a, b) == 1;
    }

    // Returns the number of integers between 1 and n that are
    // relatively prime with n.
    public static int totient(int n) {
        int count = 0;
        for (int i = 0; i < n; i++) {
            if (areRelativelyPrime(i, n)) {
                count++;
            }
        }
        return count;
    }

    public static void main(String[] args) {
        int a = Integer.parseInt(args[0]);
        int b = Integer.parseInt(args[1]);
        StdOut.println("gcd(" + a + "," + b + ") = " + gcd(a, b));
        StdOut.println("lcm(" + a + "," + b + ") = " + lcm(a, b));
        StdOut.println("areRelativelyPrime(" + a + "," + b + ") = " + areRelativelyPrime(a, b));
        StdOut.println("totient(" + a + ") = " + totient(a));
        StdOut.println("totient(" + b + ") = " + totient(b));
    }
}

Link To: Java Source Code