Coursera - Computer Science: Programming With A Purpose

A Java programmer begins walking aimlessly. At each time step, she takes one step in a random direction (either north, east, south, or west), each with probability 25%. She stops once she is at Manhattan distance r from the starting point. How many steps will the random walker take? This process is known as a two-dimensional random walk.

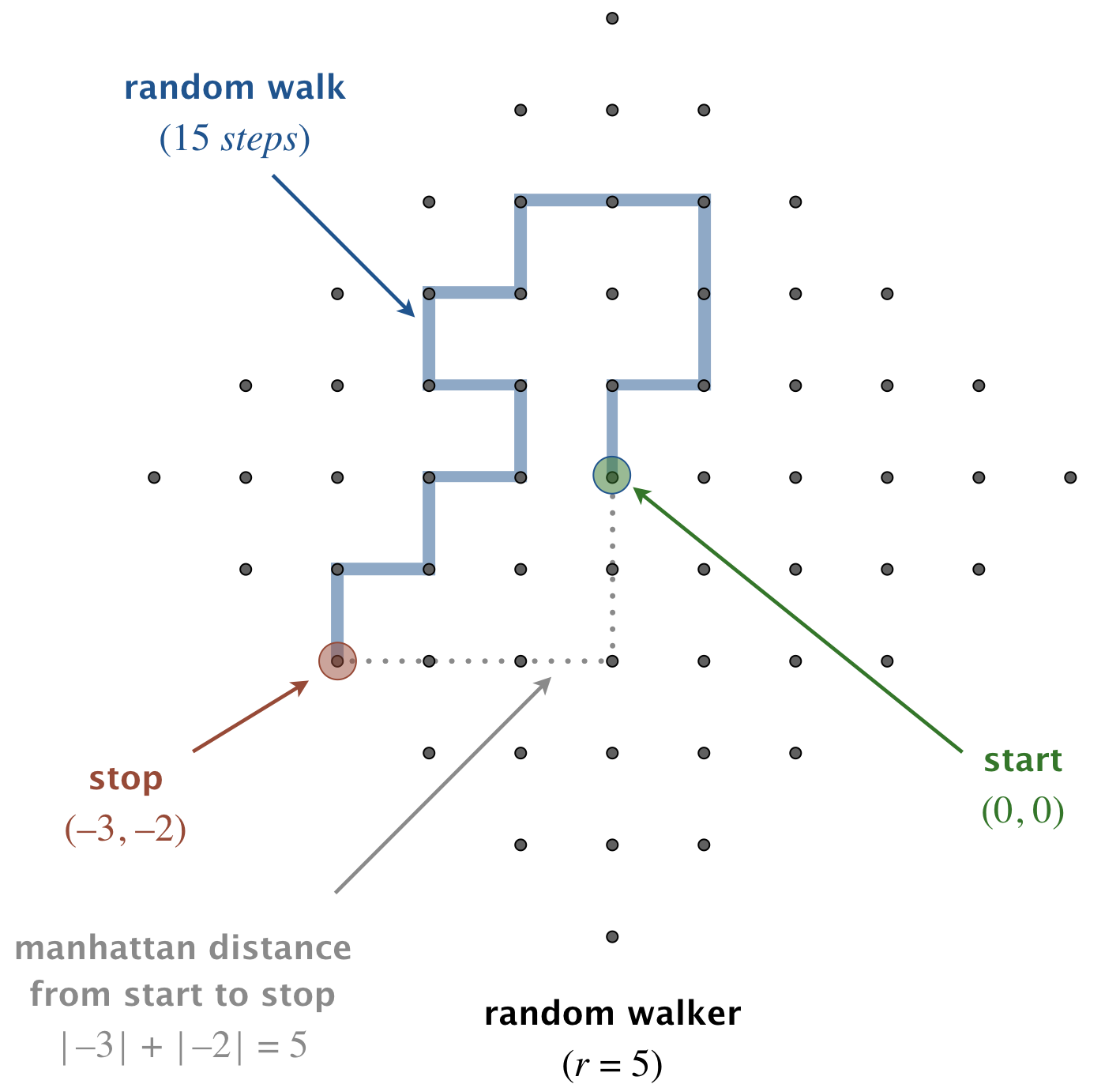
Write a program RandomWalker.java that takes an integer command-line argument r and simulates the motion of a random walk until the random walker is at Manhattan distance r from the starting point. Print the coordinates at each step of the walk (including the starting and ending points), treating the starting point as (0, 0). Also, print the total number of steps taken.

~/Desktop/loops> java RandomWalker 5
(0, 0)
(0, 1)
(1, 1)
(1, 2)
(1, 3)
(0, 3)
(-1, 3)
(-1, 2)
(-2, 2)
(-2, 1)
(-1, 1)
(-1, 0)
(-2, 0)
(-2, -1)
(-3, -1)
(-3, -2)
steps = 15

This process is a discrete version of a natural phenomenon known as Brownian motion. It serves as a scientific model for an astonishing range of physical processes from the dispersion of ink flowing in water, to the formation of polymer chains in chemistry, to cascades of neurons firing in the brain.

Note: the above description is copied from Coursera and converted to markdown for convenience

Solution:

public class RandomWalker {

    public static void main(String[] args) {
        final int r = Integer.parseInt(args[0]);

        // output starting position
        int x = 0;
        int y = 0;
        System.out.println("(" + x + "," + y + ")");

        double random = 0.0;
        int steps = 0;
        int distance = 0;
        while (distance != r) {
            random = Math.random();
            if (random < 0.25) {
                x -= 1;
            } else if (random < 0.50) {
                x += 1;
            } else if (random < 0.75) {
                y -= 1;
            } else {
                y += 1;
            }
            steps++;

            // output new position
            System.out.println("(" + x + "," + y + ")");

            // calculate new manhattan distance
            distance = Math.abs(x) + Math.abs(y);
        }
        System.out.println("steps = " + steps);
    }
}

Link To: Java Source Code