Coursera - Computer Science: Programming With A Purpose

The great-circle distance is the length of the shortest path between two points (x1, y1) and (x2, y2) on the surface of a sphere, where the path is constrained to be along the surface.

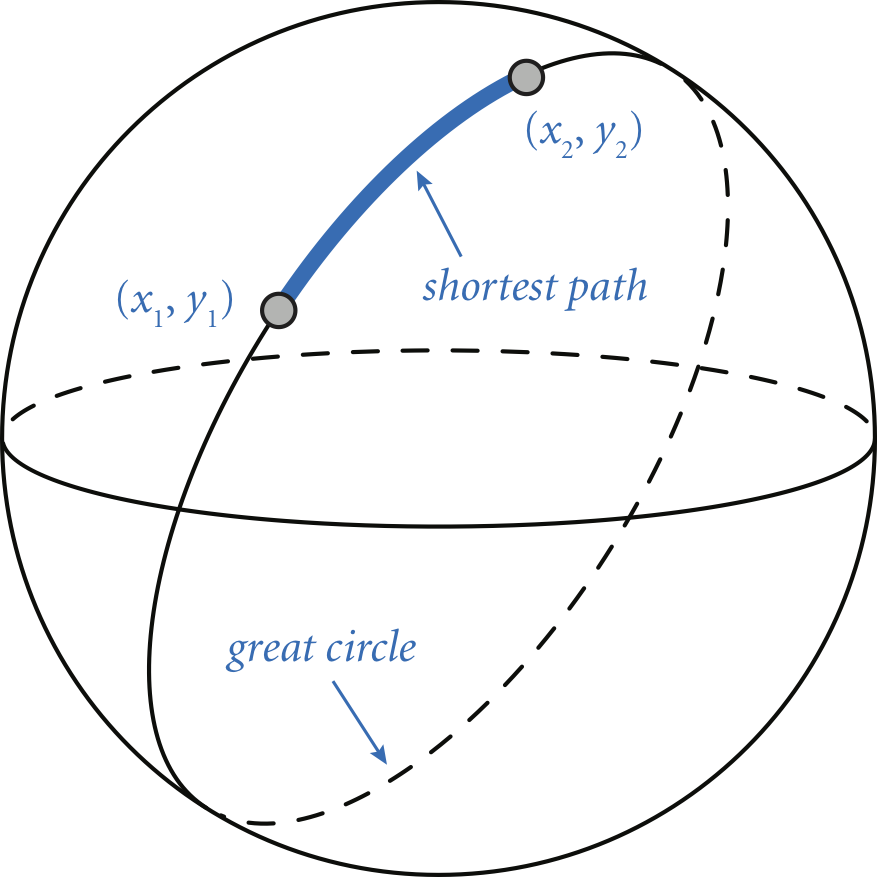
Write a program GreatCircle.java that takes four double command-line arguments x1, y1, x2, and y2 — the latitude and longitude (in degrees) of two points on the surface of the earth — and prints the great-circle distance (in kilometers) between them. Use the following Haversine formula

    distance = 2r arcsin(sqrt(sin²((x₂ - x₁)/2) + cos x₁ cos x₂ sin²((y₂ - y₁)/2)))

where r = 6,371.0 is the mean radius of the Earth (in kilometers).

~/Desktop/hello> javac GreatCircle.java

~/Desktop/hello> java GreatCircle 40.35 74.65 48.87 -2.33    // Princeton to Paris
5902.927099258561 kilometers

~/Desktop/hello> java GreatCircle 60.0 15.0 120.0 105.0      // for debugging
4604.53989281927 kilometers

Hint: The command-line arguments are given in degrees but Java’s trigonometric functions use radians. Use Math.toRadians() to convert from degrees to radians.

Although the Earth is not a perfect sphere, this formula is a good approximation to the true distance.

Note: the above description is copied from Coursera and converted to markdown for convenience

Solution:

public class GreatCircle {

    public static void main(String[] args) {
        final double x1 = Math.toRadians(Double.parseDouble(args[0]));
        final double y1 = Math.toRadians(Double.parseDouble(args[1]));
        final double x2 = Math.toRadians(Double.parseDouble(args[2]));
        final double y2 = Math.toRadians(Double.parseDouble(args[3]));

        final double sin2x = Math.sin((x2 - x1) / 2);
        final double sin2y = Math.sin((y2 - y1) / 2);
        final double twor = 2 * 6371.0;

        final double distance =
                twor * Math.asin(Math.sqrt(
                        (sin2x * sin2x) + (Math.cos(x1) * Math.cos(x2) * (sin2y * sin2y))));
        System.out.println(distance + " kilometers");
    }
}

Link To: Java Source Code